Skip to main content

复杂度

如何评判一个算法的好坏？​

一般从以下维度来评估算法的优劣

  • 正确性、可读性、健壮性（对不合理输入的反应能力和处理能力）
  • 时间复杂度（time complexity）：估算程序指令的执行次数（执行时间）
  • 空间复杂度（space complexity）：估算所需占用的存储空间

大O表示法（Big O）​

一般用大O表示法来描述复杂度，它表示的是数据规模 n 对应的复杂度

大O表示法仅仅是一种粗略的分析模型，是一种估算，能帮助我们短时间内了解一个算法的执行效率

忽略常数、系数、低阶

  • 9 >> O(1)
  • 2n + 3 >> O(n)
  • n 2 + 2n + 6 >> O(n^2 )
  • 4n^3 + 3n^2 + 22n + 100 >> O(n^3 )
  • log2n 或者log9n >> logn（对数阶一般省略底数）

根据代码评估复杂度：

    public static void test1(int n) {
        // 1
        if (n > 10) { 
            System.out.println("n > 10");
        } else if (n > 5) { // 2
            System.out.println("n > 5");
        } else {
            System.out.println("n <= 5"); 
        }
        
        // 1 + 4 + 4 + 4
        for (int i = 0; i < 4; i++) {
            System.out.println("test");
        }
        
        // 140000
        // O(1)
        // O(1)
    }

    public static void test2(int n) {
        // O(n)
        // 1 + 3n
        for (int i = 0; i < n; i++) {
            System.out.println("test");
        }
    }

    public static void test3(int n) {
        // 1 + 2n + n * (1 + 3n)
        // 1 + 2n + n + 3n^2
        // 3n^2 + 3n + 1
        // O(n^2)
        
        // O(n)
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                System.out.println("test");
            }
        }
    }

    public static void test4(int n) {
        // 1 + 2n + n * (1 + 45)
        // 1 + 2n + 46n
        // 48n + 1
        // O(n)
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < 15; j++) {
                System.out.println("test");
            }
        }
    }

    public static void test5(int n) {
        // 8 = 2^3
        // 16 = 2^4
        
        // 3 = log2(8)
        // 4 = log2(16)
        
        // 执行次数 = log2(n)
        // O(logn)
        while ((n = n / 2) > 0) {
            System.out.println("test");
        }
    }

    public static void test6(int n) {
        // log5(n)
        // O(logn)
        while ((n = n / 5) > 0) {
            System.out.println("test");
        }
    }

    public static void test7(int n) {
        // 1 + 2*log2(n) + log2(n) * (1 + 3n)
        
        // 1 + 3*log2(n) + 2 * nlog2(n)
        // O(nlogn)
        for (int i = 1; i < n; i = i * 2) {
            // 1 + 3n
            for (int j = 0; j < n; j++) {
                System.out.println("test");
            }
        }
    }

    public static void test10(int n) {
        // O(n)
        int a = 10;
        int b = 20;
        int c = a + b;
        int[] array = new int[n];
        for (int i = 0; i < array.length; i++) {
            System.out.println(array[i] + c);
        }
    }

常见的复杂度的性能比较​

常见复杂度：

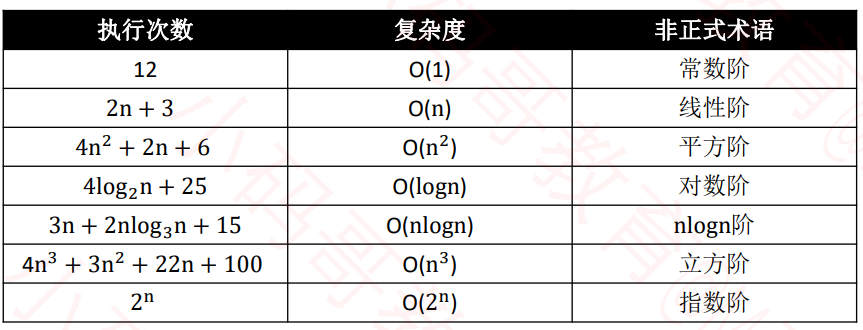
image-20220907150225896

性能比较：

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2 ) < O(n^3 ) < O(2^n ) < O(n!) < O(n^n )

数据规模较小时：

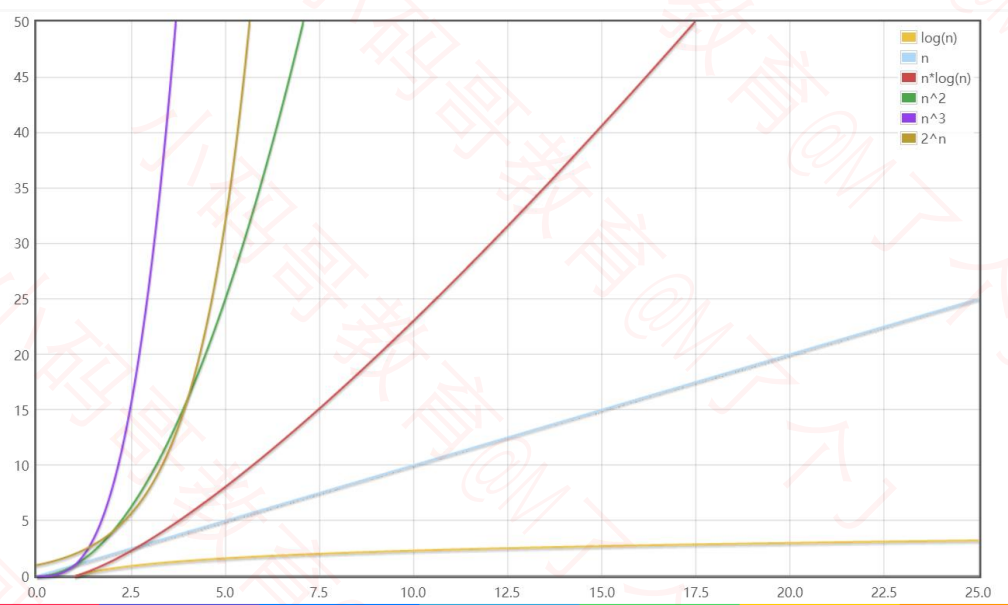
image-20220907150410244

数据规模较大时：

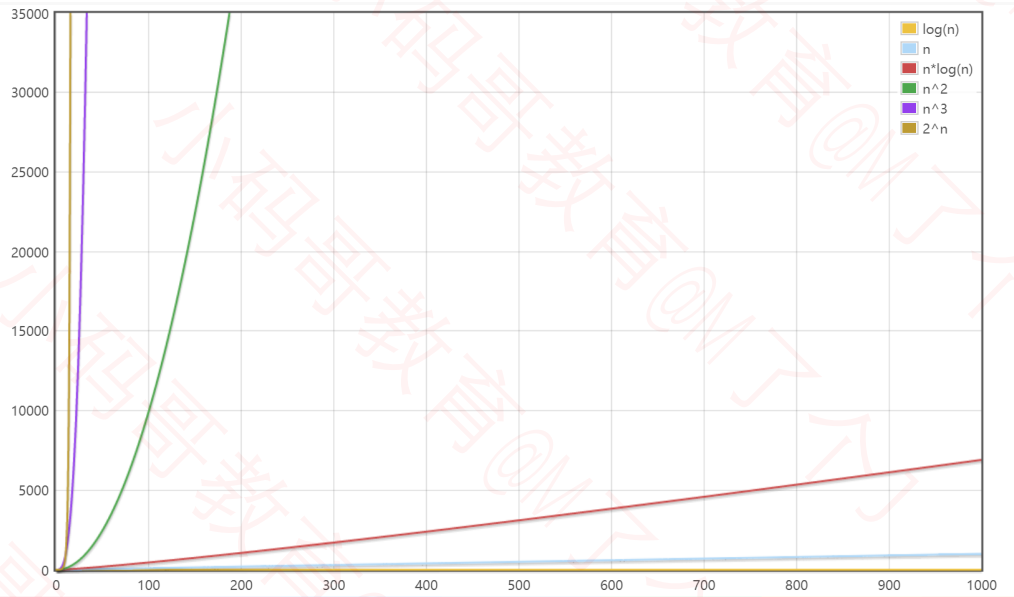
image-20220907150435748

多个数据规模的情况​

image-20220907150613127

算法的优化方向​

  • 用尽量少的存储空间

  • 用尽量少的执行步骤（执行时间）

  • 根据情况，可以

    • 空间换时间

    • 时间换空间

斐波那契数列算法的复杂度优化​

求第 n 个斐波那契数（fibonacci number），也就第n位数值是前一位和前两位数值相加。

使用递归，时间复杂度为O(2^n)

//第一种算法：使用递归
    // O(2^n)
public static int fib1(int n) {
    if (n <= 1) return n;
    return fib1(n - 1) + fib1(n - 2);
}

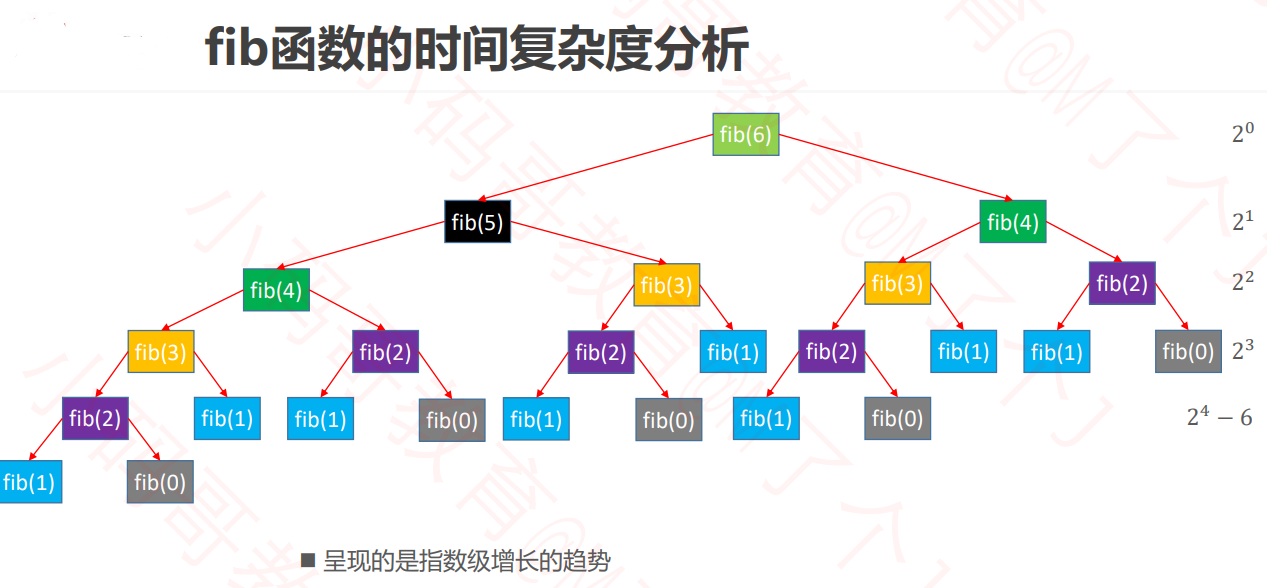
image-20220907171606545

使用循环，时间复杂度为O(n)

// O(n)
    public static int fib2(int n) {
        if (n <= 1) return n;
        
        int first = 0;
        int second = 1;
        for (int i = 0; i < n - 1; i++) {
            int sum = first + second;
            first = second;
            second = sum;
        }
        return second;
    }

使用公式，时间复杂度为O(1)

image-20220907171738177

它们的差别：

他们的差别有多大？

  • 如果有一台1GHz的普通计算机，运算速度 109 次每秒（ n 为 64 ）
  • O(n) 大约耗时 6.4 ∗ 10−8 秒
  • O(2 n ) 大约耗时 584.94 年
  • 有时候算法之间的差距，往往比硬件方面的差距还要大