Skip to main content

AVL树

AVL树​

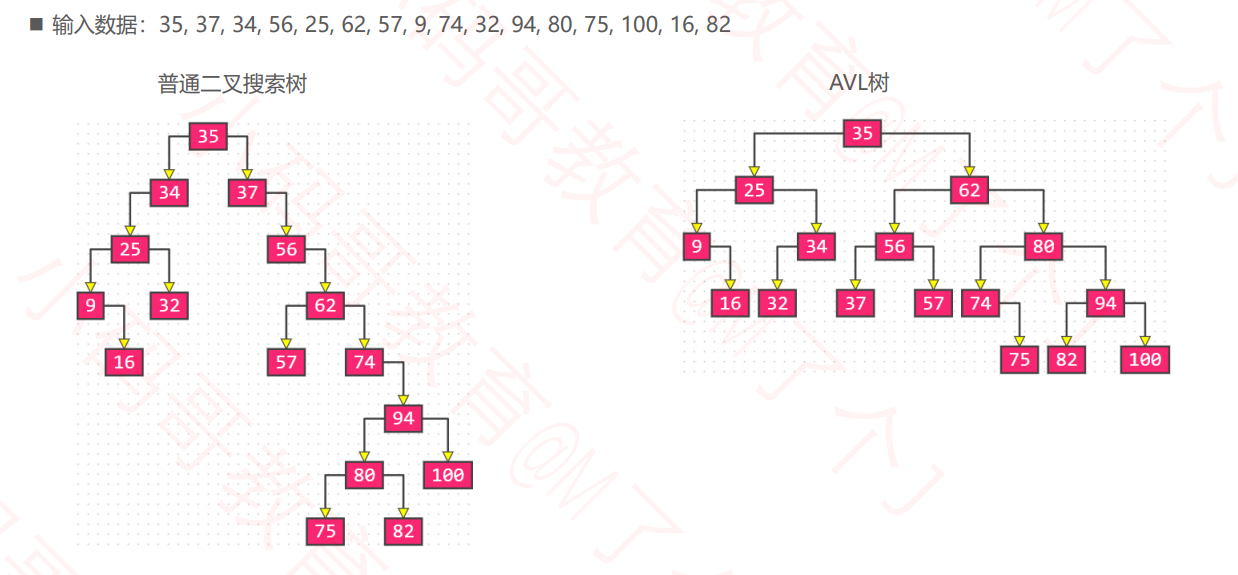
AVL树是最早发明的自平衡二叉搜索树之一

AVL 取名于两位发明者的名字 G. M. Adelson-Velsky 和 E. M. Landis（来自苏联的科学家）

特点

  • 平衡因子（Balance Factor）：某结点的左右子树的高度差
  • 每个节点的平衡因子只可能是 1、0、-1（绝对值 ≤ 1，如果超过 1，称之为“失衡”）
  • 每个节点的左右子树高度差不超过 1
  • 搜索、添加、删除的时间复杂度是 O(logn)

image-20221223101141515

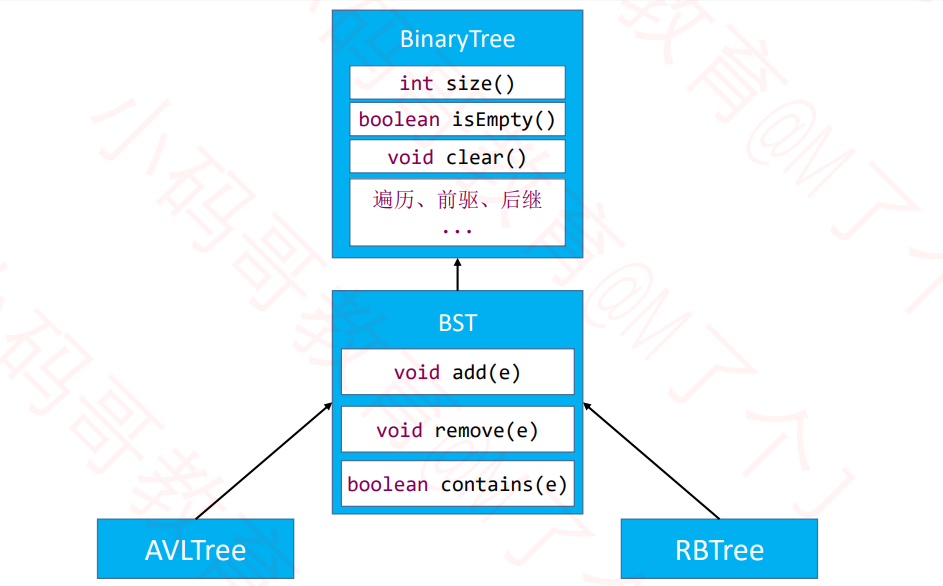
AVL树的接口设计​

int afterAdd() // 添加元素之后的平衡处理
boolean afterRemove() // 删除元素之后的平衡处理
Node<E> createNode(E element, Node<E> parent) //AVL节点与普通的二叉树节点有些区别，这里通过工厂函数返回
//AVL节点
private static class AVLNode<E> extends Node<E> {
    int height = 1;

    public AVLNode(E element, Node<E> parent) {
        super(element, parent);
    }

    public int balanceFactor() {
        int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
        int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
        return leftHeight - rightHeight;
    }

    public void updateHeight() {
        int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
        int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
        height = 1 + Math.max(leftHeight, rightHeight);
    }
    //返回左右子树中，高度最高的那个子树。如果两个子树高度相同，则返回和当前节点相同方向的子树
    //（相同方向：当前节点是在父节点的哪个左右方向）
    public Node<E> tallerChild() {
        int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
        int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
        if (leftHeight > rightHeight) return left;
        if (leftHeight < rightHeight) return right;
        return isLeftChild() ? left : right;
    }

   
}

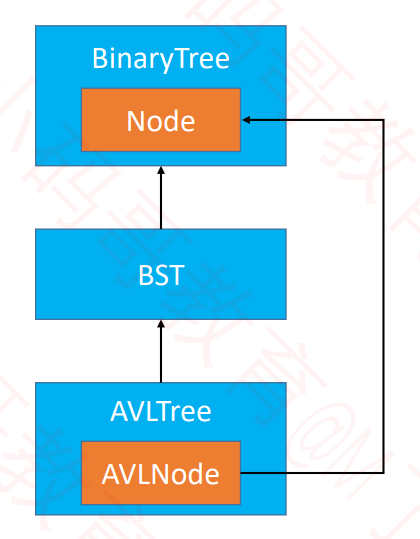
代码的继承结构

image-20221223102543581

image-20221223102700856

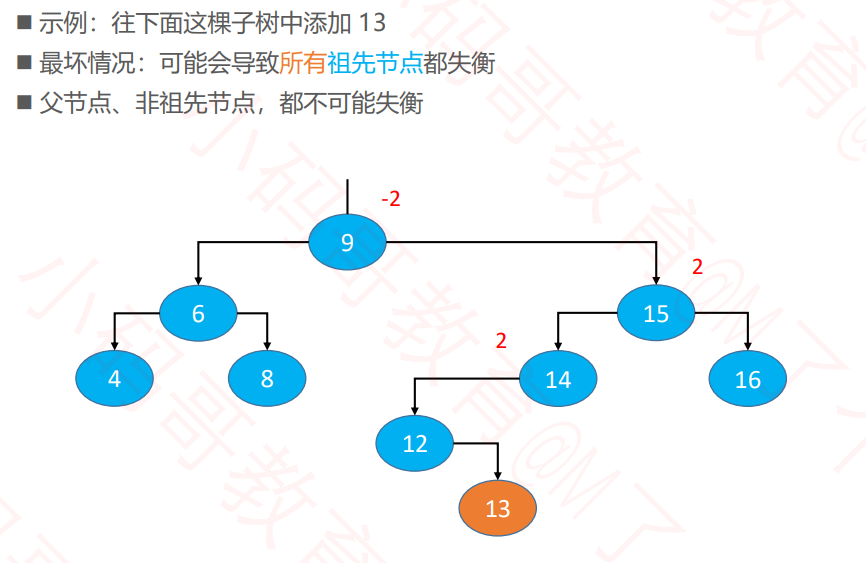
添加后的平衡操作​

添加导致的失衡​

image-20221223105241200

LL – 右旋转（单旋）​

特点

  • 失衡节点是祖父节点，也就是g。
  • 被添加的节点是在g的左边的左边。

操作-右旋转

  • g.left = p.right
  • p.right = g
  • 让p成为这棵子树的根节点
  • 维护T2、p、g 的 parent 属性
  • 先后更新 g、p 的高度

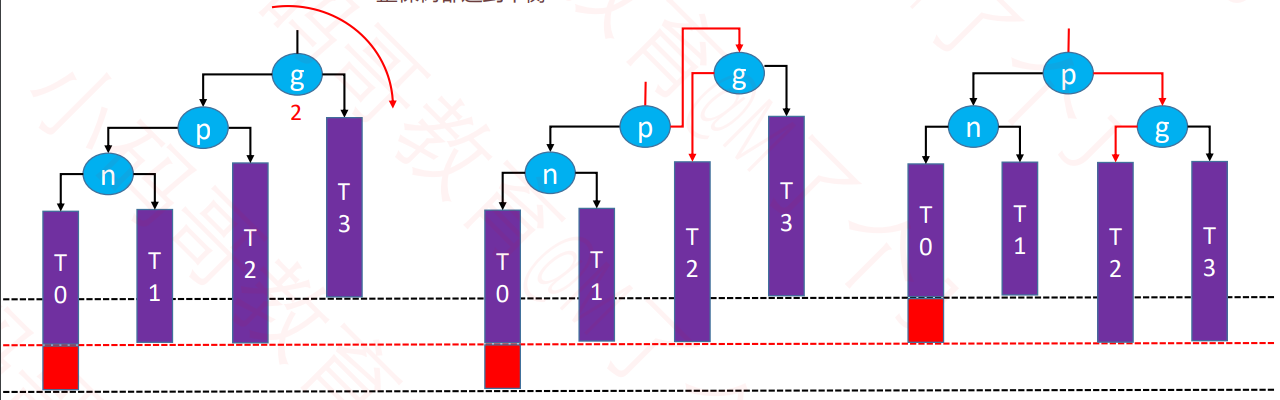
image-20221223105822088

RR – 左旋转（单旋）​

特点

  • 失衡节点是祖父节点，也就是g。
  • 被添加的节点是在g的右边的右边。

操作-左旋转

  • g.right = p.left
  • p.left = g
  • 让p成为这棵子树的根节点
  • 维护T1、p、g 的 parent 属性
  • 先后更新 g、p 的高度

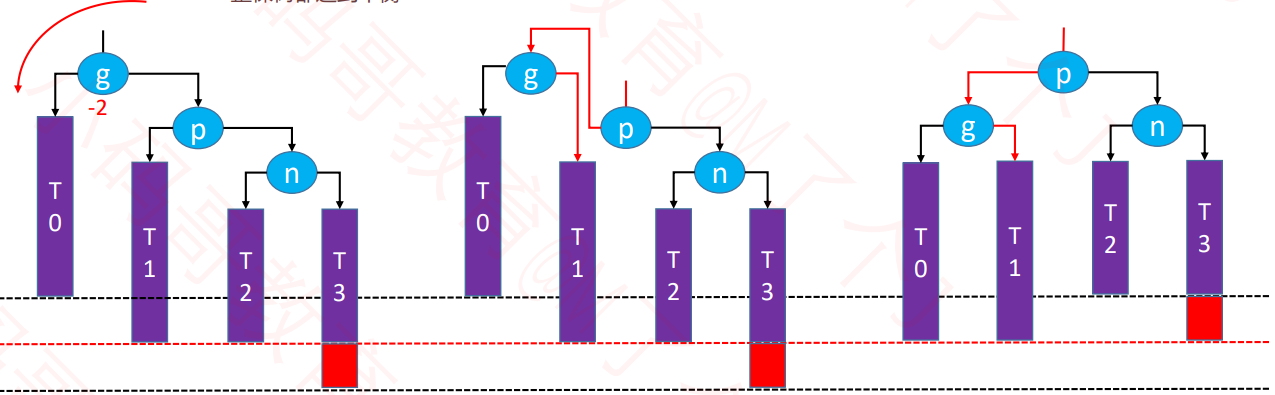
image-20221223110023288

LR – RR左旋转，LL右旋转（双旋）​

特点

  • 失衡节点是祖父节点，也就是g。
  • 被添加的节点是在g的左边的右边。

操作-先对p左旋转，再对g右旋转

  • 对p左旋转

    • p.right = n.left

    • n.left = p

    • 让n成为这棵子树的根节点

    • 维护T1、n、p的 parent 属性

    • 先后更新 n、p 的高度

  • 对g进行右旋转

    • g.left = n.right
    • n.right = g
    • 让n成为这棵子树的根节点
    • 维护T2、n、g 的 parent 属性
    • 先后更新 g、n 的高度

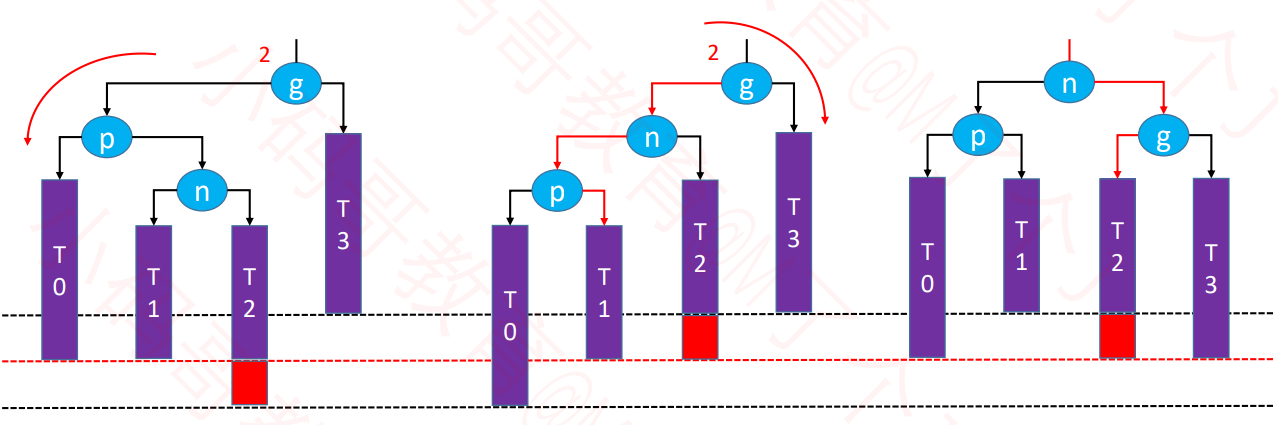
image-20221223110810997

RL – LL右旋转，RR左旋转（双旋）​

特点

  • 失衡节点是祖父节点，也就是g。
  • 被添加的节点是在g的右边的左边。

操作-先对p右旋转，再对g左旋转

  • 对p右旋转

    • p.left= n.right

    • n.right= p

    • 让n成为这棵子树的根节点

    • 维护T2、n、p的 parent 属性

    • 先后更新 n、p 的高度

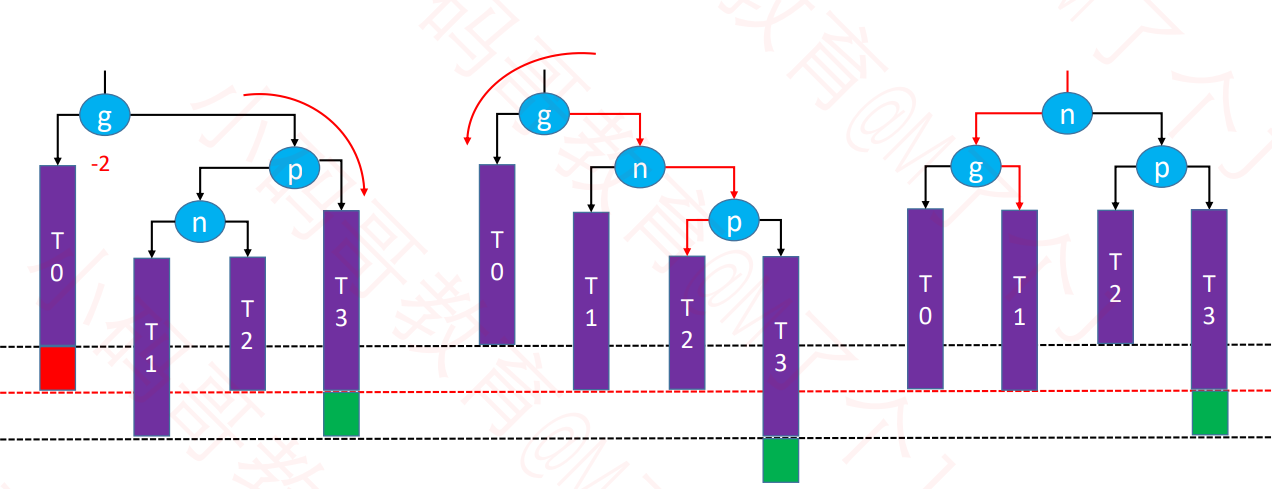
  • 对g进行左旋转

    • g.right= n.left
    • n.left= g
    • 让n成为这棵子树的根节点
    • 维护T1、n、g 的 parent 属性
    • 先后更新 g、n 的高度

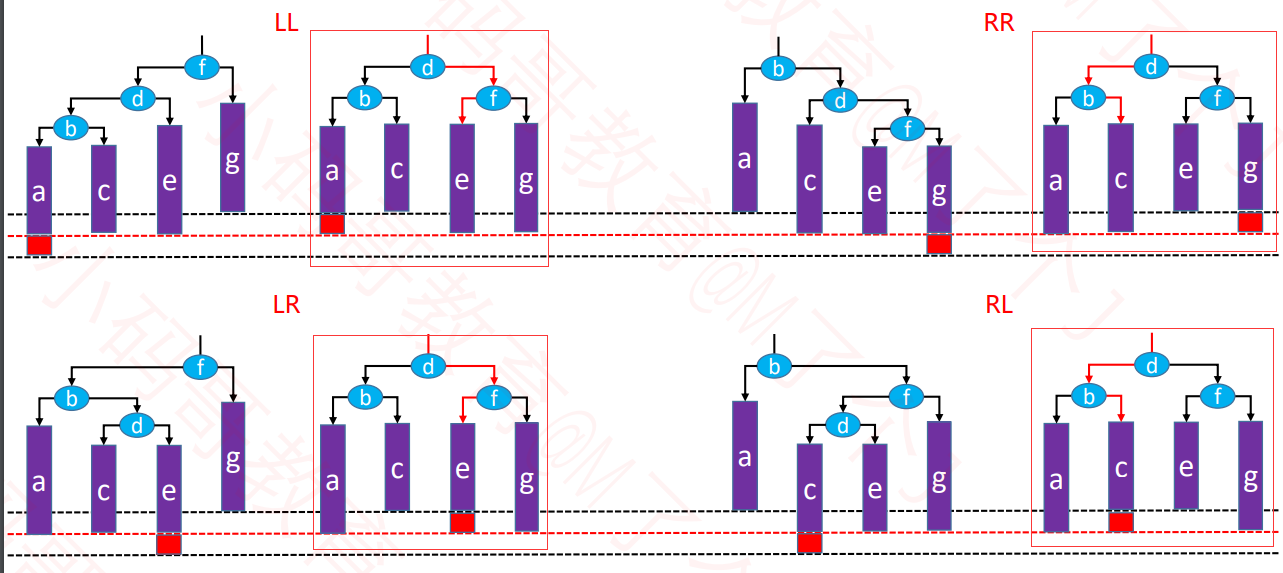
统一所有旋转操作​

  • 将所有的结点以a,b……从小到大命名
  • 我们可以发现，无论是LL,RR,LR,RL哪一种旋律，最终都会得到一样的结果。
  • 那我们就可以在输入的时候，确定a,b,c……是哪一个节点，就可以不用旋律，直接操作。

image-20221223111830469

删除后的平衡操作​

删除导致的失衡​

image-20221223112044949

LL – 右旋转（单旋）​

  • 如果绿色节点不存在，更高层的祖先节点可能也会失衡，需要再次恢复平衡，然后又可能导致更高层的祖先节点失衡...
  • 极端情况下，所有祖先节点都需要进行恢复平衡的操作，共 O(logn) 次调整

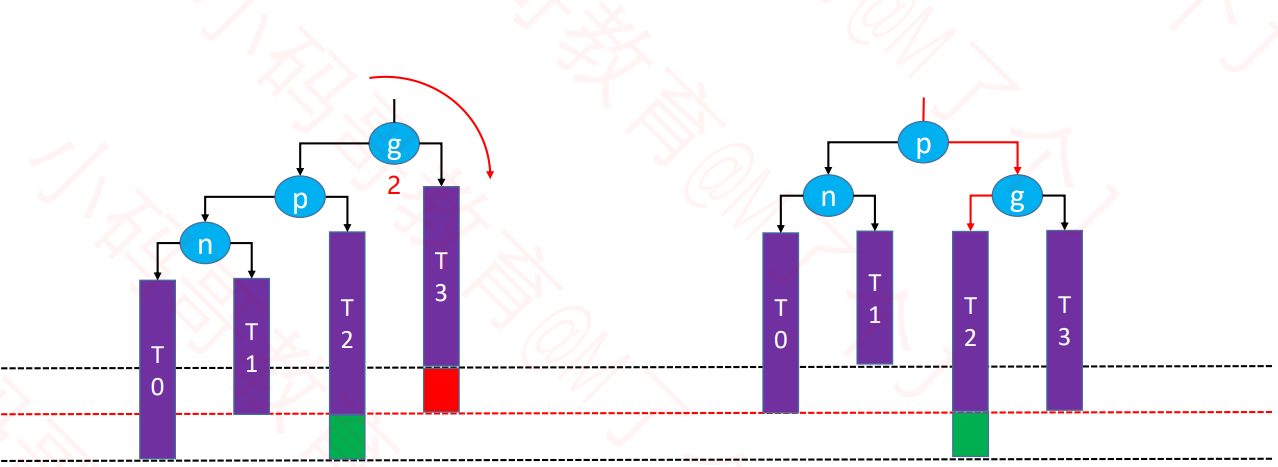
image-20221223112213605

RR – 左旋转（单旋）​

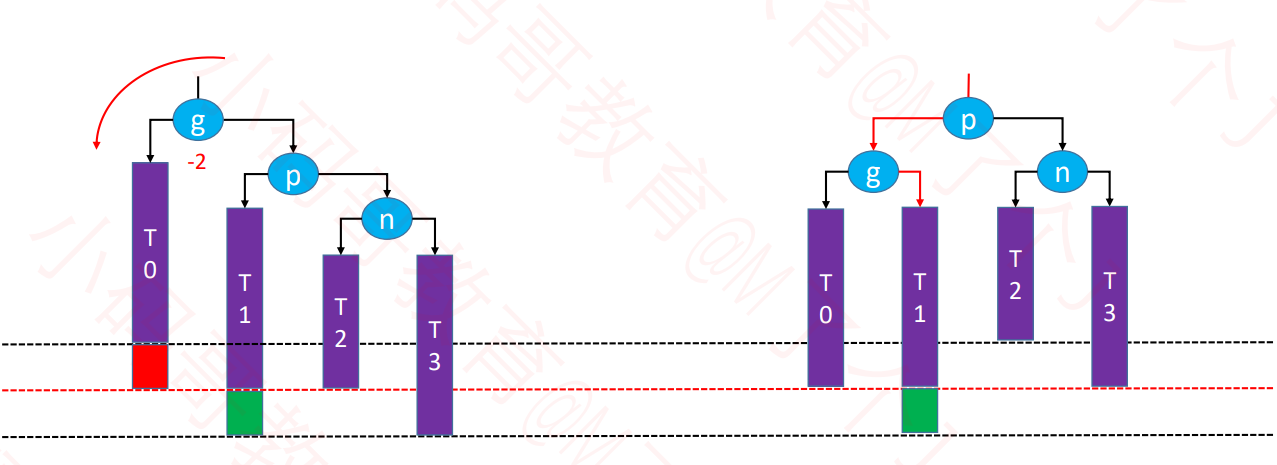
image-20221223112241362

LR – RR左旋转，LL右旋转（双旋）​

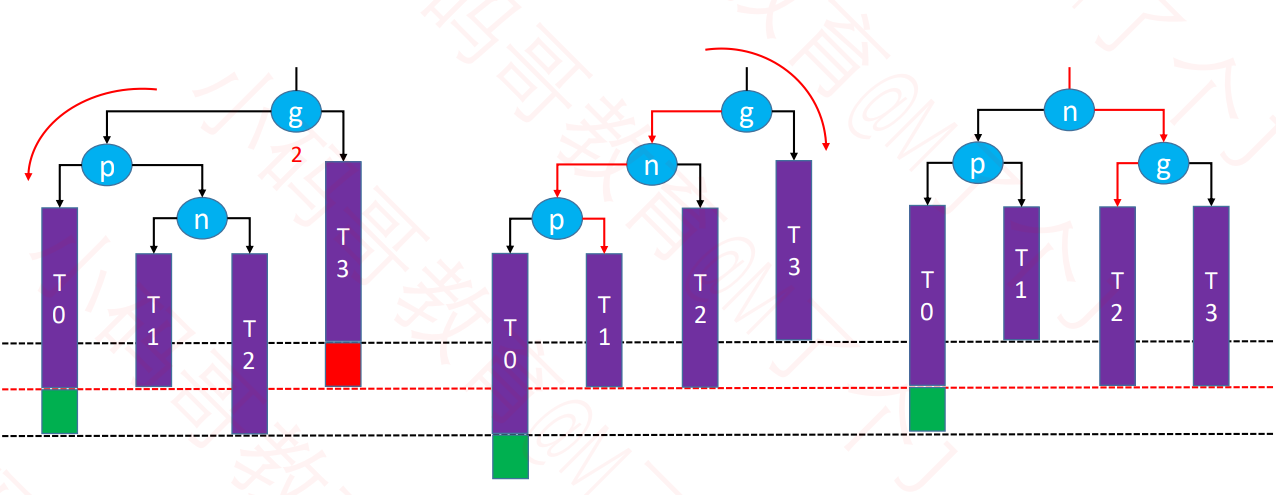
image-20221223112301550

RL – LL右旋转，RR左旋转（双旋）​

image-20221223112326030

zig、zag​

有些教程里面

把右旋转叫做zig，旋转之后的状态叫做zigged

把左旋转叫做zag，旋转之后的状态叫做zagged

总结​

  • 添加
    • 可能会导致所有祖先节点都失衡
    • 只要让高度最低的失衡节点恢复平衡，整棵树就恢复平衡【仅需 O(1) 次调整】
  • 删除
    • 可能会导致父节点或祖先节点失衡（只有1个节点会失衡）
    • 恢复平衡后，可能会导致更高层的祖先节点失衡【最多需要 O(logn) 次调整】
  • 平均时间复杂度
    • 搜索：O(logn)
    • 添加：O(logn)，仅需 O(1) 次的旋转操作
    • 删除：O(logn)，最多需要 O(logn) 次的旋转操作

作业​

平衡二叉树：https://leetcode-cn.com/problems/balanced-binary-tree/