动态数组

什么是数据结构？

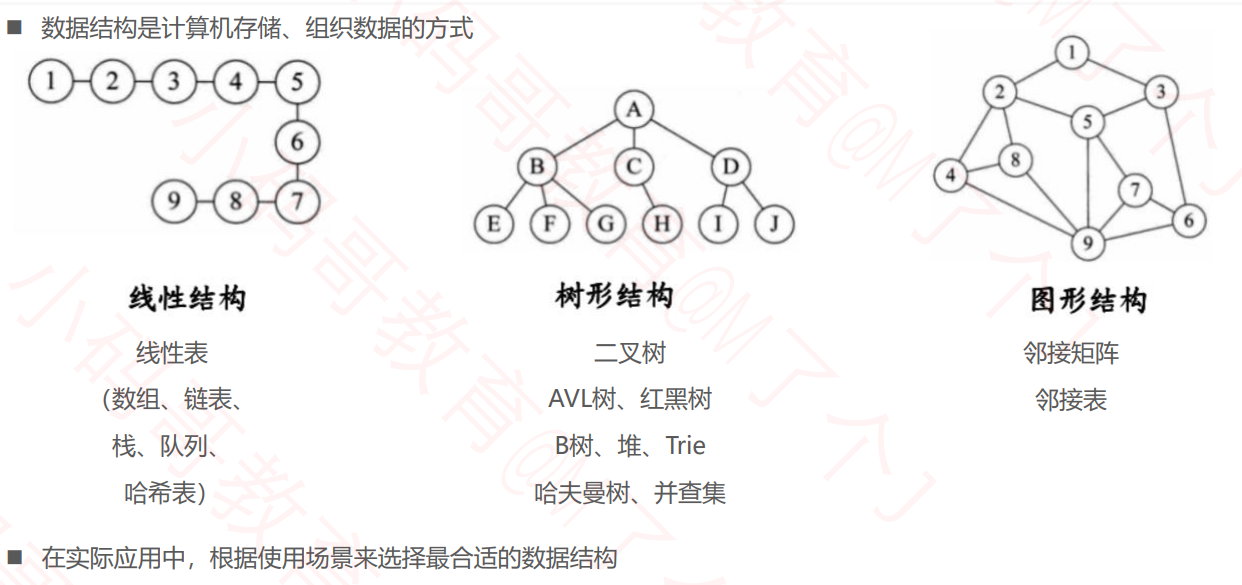
线性表

数组（Array）

动态数组（Dynamic Array）接口设计

• int size(); // 元素的数量
• boolean isEmpty(); // 是否为空
• boolean contains(E element); // 是否包含某个元素
• void add(E element); // 添加元素到最后面
• E get(int index); // 返回index位置对应的元素
• E set(int index, E element); // 设置index位置的元素
• void add(int index, E element); // 往index位置添加元素
• E remove(int index); // 删除index位置对应的元素
• int indexOf(E element); // 查看元素的位置
• void clear(); // 清除所有元素

动态数组复杂度分析

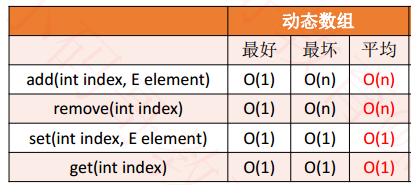
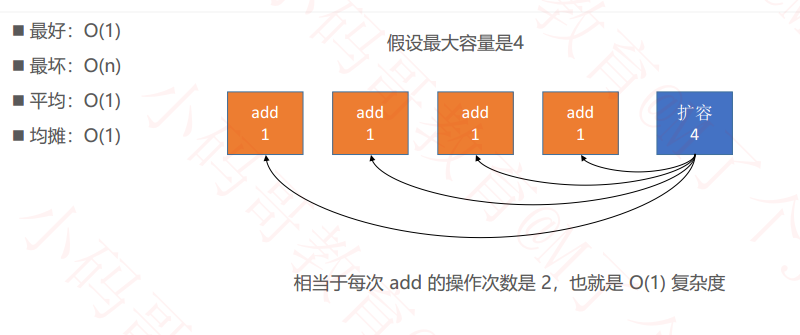
动态数组均摊复杂度

什么情况下适合使用均摊复杂度：

• 经过连续的多次复杂度比较低的情况后，出现个别复杂度比较高的情况
• 比如add函数，add(E element) 平均都是添加一个，但是如果遇到扩容的时候，就会变成O(n)，复杂度陡然上升。但是把O(n)的复杂度平均给前面的每一个，均摊复杂度 就是O(1)

动态数组代码实现

@SuppressWarnings("unchecked")
public class ArrayList<E> extends AbstractList<E> {
    /**
     * 所有的元素
     */
    private E[] elements;
    private static final int DEFAULT_CAPACITY = 10;
    
    public ArrayList(int capaticy) {
        capaticy = (capaticy < DEFAULT_CAPACITY) ? DEFAULT_CAPACITY : capaticy;
        elements = (E[]) new Object[capaticy];
    }
    
    public ArrayList() {
        this(DEFAULT_CAPACITY);
    }
    
    /**
     * 清除所有元素
     */
    public void clear() {
        for (int i = 0; i < size; i++) {
            elements[i] = null;
        }
        size = 0;
    }

    /**
     * 获取index位置的元素
     * @param index
     * @return
     */
    public E get(int index) { // O(1)
        rangeCheck(index);
        
        return elements[index]; 
    }

    /**
     * 设置index位置的元素
     * @param index
     * @param element
     * @return 原来的元素ֵ
     */
    public E set(int index, E element) { // O(1)
        rangeCheck(index);
        
        E old = elements[index];
        elements[index] = element;
        return old;
    }

    /**
     * 在index位置插入一个元素
     * @param index
     * @param element
     */
    public void add(int index, E element) { 
        /*
         * 最好：O(1)
         * 最坏：O(n)
         * 平均：O(n)
         */
        rangeCheckForAdd(index);
        
        ensureCapacity(size + 1);
        
        for (int i = size; i > index; i--) {
            elements[i] = elements[i - 1];
        }
        elements[index] = element;
        size++;
    } // size是数据规模

    /**
     * 删除index位置的元素
     * @param index
     * @return
     */
    public E remove(int index) {
        /*
         * 最好：O(1)
         * 最坏：O(n)
         * 平均：O(n)
         */
        rangeCheck(index);
        
        E old = elements[index];
        for (int i = index + 1; i < size; i++) {
            elements[i - 1] = elements[i];
        }
        elements[--size] = null;
        return old;
    }

    /**
     * 查看元素的索引
     * @param element
     * @return
     */
    public int indexOf(E element) {
        if (element == null) {
            for (int i = 0; i < size; i++) {
                if (elements[i] == null) return i;
            }
        } else {
            for (int i = 0; i < size; i++) {
                if (element.equals(elements[i])) return i;
            }
        }
        return ELEMENT_NOT_FOUND;
    }
    
    /**
     * 保证要有capacity的容量
     * @param capacity
     */
    private void ensureCapacity(int capacity) {
        int oldCapacity = elements.length;
        if (oldCapacity >= capacity) return;
        
        // 新容量为旧容量的1.5倍
        int newCapacity = oldCapacity + (oldCapacity >> 1);
        E[] newElements = (E[]) new Object[newCapacity];
        for (int i = 0; i < size; i++) {
            newElements[i] = elements[i];
        }
        elements = newElements;
        
        System.out.println(oldCapacity + "扩容为" + newCapacity);
    }
    
    @Override
    public String toString() {
        // size=3, [99, 88, 77]
        StringBuilder string = new StringBuilder();
        string.append("size=").append(size).append(", [");
        for (int i = 0; i < size; i++) {
            if (i != 0) {
                string.append(", ");
            }
            
            string.append(elements[i]);
            
//          if (i != size - 1) {
//              string.append(", ");
//          }
        }
        string.append("]");
        return string.toString();
    }
}

动态数组的优化

动态数组的缩容

如果内存使用比较紧张，动态数组有比较多的剩余空间，可以考虑进行缩容操作

• 比如剩余空间占总容量的一半时，就进行缩容
• 如果扩容倍数、缩容时机设计不得当，有可能会导致复杂度震荡 。比如扩容与缩容都是一倍，那么频繁添加或删除最后一个时间，会一时扩容，一时缩容。

@Override
public E remove(int index) {
      //....
        trim();
      //....
 }
   private void trim() {
        // 30
        int oldCapacity = elements.length;
        // 1/3
        int newCapacity = oldCapacity /3;
        if (size > (newCapacity) || oldCapacity <= DEFAULT_CAPACITY) return;
        
        // 剩余空间还很多
        E[] newElements = (E[]) new Object[newCapacity];
        for (int i = 0; i < size; i++) {
            newElements[i] = elements[i];
        }
        elements = newElements;
        
        System.out.println(oldCapacity + "缩容为" + newCapacity);
    }